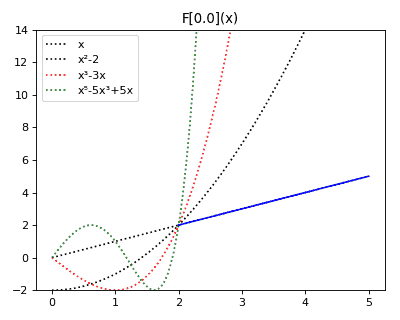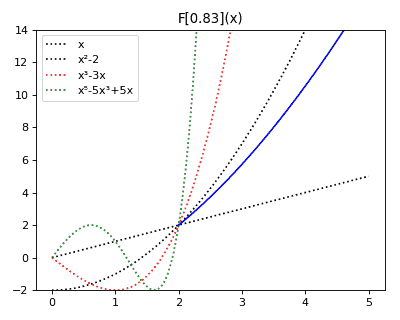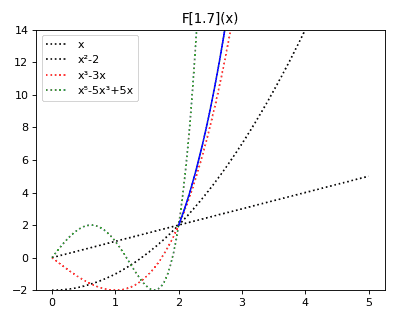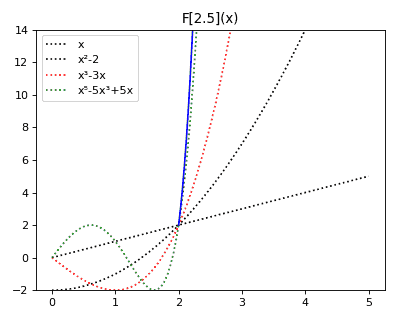
Anticategories theory
Let me to share to you a toy construction, that kept me entertained recently. Without a better idea, I dubbed it "theory of anticategories". I constructed it definition-first, starting from abstract definitions and ending with discovering examples of such objects and their relation with groupoids. I enjoyed the process of writing it, and hope someone could enjoy reading it (or glossing it over). Indeed, I understand that it is not something deep, the whole construction was done as entertainment after reading an introduction into category theory. People on Reddit suggested that this construction resembles spans . Indeed, the resemblance is striking! However, I feel that spans theory is much deeper. Seems that I described some special kind of spans. I wrote the original document and drew diagrams using Mathcha editor, but then semi-manually converted it to HTML with Mathjax to post it here. Definition Let's define an anticategory is a collecti...