The Single Rotation rule: remarkably simple and rich reversible cellular automaton
See also other posts tagged Single Rotation.
In the previous post I have presented the Reversible Cellular Automata simulator, along with some explanations about the reversible computations and block cellular automata. This post is dedicated to the specific reversible cellular automaton, I have stumbled upon while playing with the Simulator: the “Single Rotation” rule. Here is what it looks like:
Your browser must support SVG and JavaScript to show the animation above. In case your browser does not support it, see the GIF animation:

This automaton is an example of the binary block cellular automaton with Margouls neighborhood. It can be described by the only one simple block transition rule:
Rotate clockwise by 90° every block with exactly 1 alive cell.And that's all: other blocks remain unchanged. The numeric code for this rule is: [0,2,8,3,1,5,6,7,4,9,10,11,12,13,14,15], which corresponds to the following substitution table:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 8 | 3 | 1 | 5 | 6 | 7 | 4 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Time-reversibility of this rule is obvious: previous state can be obtained by reversing the direction of the rotation. Just like the famous “Game of Life”, this rule is very simple, but the automaton it defines has a remarkably complex behavior, arguably more rich than that of the “Critters” rule ([1], [2]), better covered in the net. I doubt that I am the first one to discover this rule (the rule is too simple), but I haven't seen it mentioned anywhere, so - who knows?
Properties of the “Single Rotation” rule
Conservation of population
The rule has a simple conservation law: evolution of the field never changes the total number of the alive cells. This immediately follows from the transfer function, since rotation obviously never changes total number of alive cells.
No mirror symmetry
Unlike the irreversible “Game of Life” and reversible rule “Critters”, “Single Rotation” rule has no mirror symmetry. Mirrored patterns will evolve absolutely differently from the original. The symmetries “Single Rotation” universe is invariant to are:
- Rotation by 90°, and, consequently, rotations by 180° and 270°.
- Translation by 2n cells along coordinate axes. Note that translation by 1 cell will also change the evolution of a pattern.
Patterns
As a consequence of the time-reversibility, no pattern can completely disappear (die out) in the reversible CA. Moreover, population invariance prohibits patterns that grow infinitely: guns, puffers and breeders. Reactions, that consume spaceships are also impossible.
By the above reasons, pattern types in the “Single Rotation” rule are limited to spaceships and oscillators (including static lifes as a special kind). Boring? Not at all, because their variety is extremely rich.
Spaceships!
For me, spaceships always were the most interesting kind of the patterns. And “Single Rotation” universe has a whole zoo of them, with different velocities, periods and directions. I've discovered 90 different spaceships, naturally produced by a random reaction. For comparison: in the “Game of Life” there are 2 spaceships that appear naturally in the random reactions: the Glider and the LWSS, with the latter being rare. In the “Critters” rule, there is one common light spaceship (“brace”, RLE: $2bo$bo$bo$2bo ) and few rare spaceships. See the collection of the “Critters” spaceships in the Simulator.


Lightest spaceships
Spaceships of the minimal possible “weight” (number of alive cells) play special role in the reversible CAs with conservation. In the “Single Rotation” rule every pattern with 1,2,or 3 cells is an oscillator. A spaceship must have at least 4 alive cells. (This should be easily provable by enumeration) There are 6 different 4-cell spaceships, 1 orthogonal and 5 diagonal ones:

Spaceship “A” is the only 4-cell spaceship that moves in the orthogonal direction. It has period 12 and velocity c/6. I am conjecturing that it is also the fastest spaceship possible. However, this is only a hypothesis, I don't have a proof. Big spaceships can sometimes be unexpectedly fast, for example, the second fastest known to me orthogonal spaceship has 9 cells.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| Type | Orthogonal | Diagonal | Diagonal | Diagonal | Diagonal | Diagonal |
| Period | 12 | 28 | 44 | 48 | 61 | 368 |
| Translation | 2 | 2 | 2 | 2 | 1 | 2 |
| Velocity | c/6 | c/14 | c/22 | c/24 | c/61 | c/184 |
| Natural abundance | 0.242 | 0.308 | 0.191 | 0.159 | 0.041 | 0.036 |
The spaceship “F”, resembling a vertical stroke has unexpectedly large period: 368 generations, which makes it one of the slowest spaceships.
Lightest spaceships has several special properties. One of them can be formulated as a theorem:
Theorem:See demonstration below. Note that the interaction can move the single cell, and the type of the spaceship can change.
Collision of a lightest spaceship with a single cell always produces single cell and another lightest spaceship.

Conway's Glider
I believe that it is nothing more than a curious coincidence, but the iconic Conway's GOL Glider is also a spaceship in the “Single Rotation” universe. It has period 15, translating diagonally by 2 cells every period. It is rather common spaceship, its natural abundance is 0.009 that means that roughly every 100'th spaceship produced by the random reaction is a Conway's Glider.
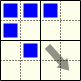
Important note here: since “Single Rotation” universe is not invariant under mirror flips and translations by an odd amount, it is important to correctly align the pattern to the blocks.
Oscillators
In the Reversible Cellular Automata, every non-growing pattern that is not a spaceship is an oscillator. It is easy to prove that under the rule with population conservation, every pattern is either an oscillator, a spaceship or will eventually evolve in the combination of the first two.
The smallest oscillator is a single cell, which have period 4 and rotates clockwise or counter-clockwise depending on the initial position. There are 2 possible 2-cell oscillators and several 3-cell ones.

Indestructible Still lifes (period-1 oscillators)
Still lifes are easy to construct in the “Single Rotation” rule: construct a pattern that have 2 or more alive cells in every block, regardless of the subdivision phase.
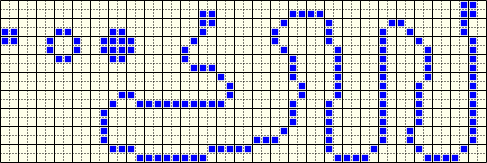
Interestingly, such patterns are indestructible: no interaction could ever change them. Since the rule is time-reversible, indestructibility leads to inconstructibility: such patterns could never arise during interaction.
Static lifes can be used to construct impenetrable walls, enclosing parts of the field. When a spaceship collides with such indestructible object, it gets “smashed” into a cloud of chaotically moving cells that are orbiting the obstacle's indestructible core, but then this cloud inevitably produces another spaceship. See example:

In this experiment, lightest orthogonal spaceship collides with a static life and “bounces” from it. It is not a coincidence, there is a general property that can be formulated as a theorem, similar to the previous one:
Theorem:Note that the kind of the spaceship can change during the interaction (in the animation above it does not change though). There is one difference with a previous theorem regarding the single-cell collision: position of the single cell can change, but position of the still life would be exactly the same.
In the “Single Rotation” cellular automaton, collision of a lightest spaceship with a static life always produces another lightest spaceship and the same static life.
There are several other theorems about the “Single Rotation” universe. I'll write about them later. Maybe.
Code and Programs
Animated SVG demo
The animation at the top of the post was made with SVG image, animated by the means of JavaScript. The sources are available in the same GitHub repository: dmishin/js-revca.
It does not simply plays the animation, it actually simulates the automaton, and the initial pattern as well as other animation parameters can be specified via URL arguments. See some examples:
- The second fastest orthogonal spaceship, played without intermediate animation steps.
-
The lightest spaceship “F” (slowest), played quickly without intermediate steps.
You'll need to wait 368 steps to see it translated by 2 cells. - The fastest orthogonal spaceship “A”. With the same speed settings as the previous one.
- The same, but slower and including intermediate animation steps.
- A rare heavy diagonal 9-cell spaceship.
SVG demo should work in the most of the modern browsers, desktop and mobile.

Comments
Why would such a rule be interesting? The reason is that we can use *local orientations* as cell states. Then the two rules can be seen as one rule as follows:
Rule: In a block, if there is exactly one cell of a given orientation in that block, rotate the block 90 degrees clockwise, using that orientation's definition of clockwise.
If we are on an orientable surface (like the plane or torus) this is not particularly interesting, but if we are on a *non*orientable surface (like a mobius strip or a klein bottle), it is pretty neat. When a surface is nonorientable, there is no globally consistent orientation. That means that if a spaceship, for example, loops around the space, it will actually be in the opposite state of what it started as.
Here is a link to the simulator with this rule (I also initialized half of the field with alive cells):
http://dmishin.github.io/js-revca/?rule=0,2,8,3,1,5,6,13,4,9,10,7,12,14,11,15&rle_x0=30&rle_y0=0&rle=33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o$33o&step=8&frame_delay=100&size=64x64&cell_size=4,1&phase=0
On the first glance, it is not much different. There are no indestructible still lifes though.
For the regular Margolus neighborhood, one could also consider a rule in which every block is rotated by 90 degrees times the number of ON cells. Thus, blocks with 0 or 4 cells are unchanged, blocks with 1 on cell are rotated 90, blocks with 3 on cells are rotated 270, and (here’s where new behavior appears!) blocks with 2 cells of each type are rotated by 180. This rule is bound to give very different behavior from the ordinary single rotation rule, due to the frequency with which two-on, two-off blocks appear in most would-be spaceships.
Finally, higher-dimensional versions could be worth considering. Using the four-dimensional version of the Margolus neighborhood, for example, you could have a rule with two different types of ON cell corresponding to rotations about two orthogonal planes (planes oriented so that rotations through them commute). Thus if a block has 1 red cell and 1 blue cell, it’s rotated 90 degrees in the “red” plane and 90 degrees in the orthogonal (“blue”) plane. A “purple” cell would count towards both planes, etc. The number of variations on this rule is practically endless. 4D works much better than 3D for these types of rules because in 3D there is no way to make rotations in different planes commute.
Until trying Double Rotate, I thought that Critters was the most pleasing known reversible cellular automaton, what with it being one of the few that has a Wikipedia page, but now Double Rotate seems to me the clear champion.
A Turing machine is a finite state machine plus a tape, where the tape can be finite length at each moment, but grow arbitrarily long as it is written to. But that's equivalent to a FSM plus two stacks (if you cut the tape at the head, and tilt each half up). And if you think of the stack as encoding a binary number, then that's equivalent to a FSM plus 4 counters, where a counter is a nonnegative integer that can grow arbitrarily large, and the FSM can increment, decrement, and check if it's zero. And that, in turn (by encoding as the product of powers of 4 primes) is equivalent to a FSM plus just 2 counters.
So all you need is the ability to create two counters. There could be a main blob that is the FSM. Then a non-moving cycler that is far to the north, and another that is far to the east. If the FSM could shoot a spaceship at a blob that has the effect of moving it slightly farther away, or shoot a different spaceship that moves it slightly closer, and have a third interaction that detects whether it has retracted all the way back to the main blob, then this is equivalent to a FSM plus two counters. Which, in turn, is equivalent to a Turing machine.
In other words, you don't need infinite live cells. You just need infinite space into which your two finite patterns can move.
So the first step in building a Turing machine in this CA is to discover whether it is possible to have some pattern that oscillates in place, but when hit by some type of spaceship from a given direction, will interact with it and move slightly toward the direction the spaceship came from. And if there's another spaceship that would make it move slightly further away. Is this possible?
I'm now very curious: is this CA Turing complete?
This is exactly the proof of the Turing completness of the Game of Life that I read in the 1980s. It assumed an infinite empty universe, with a number of active cells that is always below a fixed constant, but used the distances to two remote blobs to encode an arbitrary, growing tape.
It would be very cool if that could be proved for this CA, too.
Morita, Kenichi. "Making reversible computing machines in a reversible cellular space." Bulletin of EATCS 140, no. 2 (2023).
(I would link it since the PDF is available online, but sometimes links run into trouble with spam detection.)