New Single Rotation spaceships
I still continue leisurely exploring the Single Rotation celluar automaton, a very simple reversible cellular automaton with complex emergent behavior. This post is a status repost on spaceships.
Brute-force spaceship search
My original library of spaceships had 205 patterns, found using random reaction method. Using a simple brute-force algorithm (C++ sources), some more spaceships having from 6 to 12 cells were discovered (well, this is an old news, but I haven't published it in the blog yet). Currently, there are 328 patterns in the library. The heaviest spaceship so far has 12 cells, and is surprisingly fast: c/71. For 13 cell patterns, several days of brute-forcing did not brought a single pattern yet. No knightships were found too.
Expansible spaceship
For me, this pattern is the most exciting discovery. While looking at the spaceship table, I have accidentally noticed a 7-cell spaceship, whose evolution resembled a ball, bouncing between 2 reflectors. A quick check showed that this impression was right: it consists of the lightest spaceship B, bouncing between 2 reflectors, of 1 and 2 cells. Each bounce moves the reflectors forward by 1 cell, thus making the pattern a single slow spaceship. The distance between the reflectors can be expanded, giving an infinite family of more and more slow and sparse spaceships. Note: because "Single Rotation" rule is chiral (i.e. not invariant to reflection), top and bottom reflectors must be different.
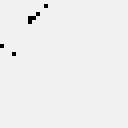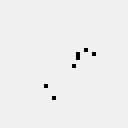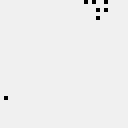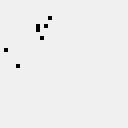
Position of the reflector may be moved by \(2k\) cells diagonally, where \(k=0,1,...\), giving a diagonal spaceship of period \(245+56k\) and translation (1,1).

An interesting challenge is to find a growing variation of the ping pong ship (that would not be a spaceship, in a strict sence). If discovered, it would be the first growing pattern with growth rate below O(n).
Spaceship chains
Another (rater old) discovery, made by staring at the spaceship catalog. There are 2 patterns of 8 cells, resembling a pair of lightest 4-cell spaceships, moving in the same direction. However, the parts are not independent, they interact during the pattern evolution (though the interaction does not change period or speed of the pattern). A quick check revealed that both these patterns can be expanded, giving 2 infinite families of long spaceships of equal period and velocity.
Fast chain spaceship
Fast chain spaceships are built from the lightest spaceship B (the table of all lightest spaceships is here). The dimer of this spaceship is produced in random reaction with probability around \(2\cdot10^{-6}\)).

New spaceships can be attached to the end of the chain in 2 ways, giving 2 possible slants. All these chains have period 28 and move diagonally with velocity c/14.

The chains can be built by the following procedure:
- Take a dimer of the spaceship B, in some phase.
- Evaluate it step by step, until its right part will have the same configuration as the left part of the original dimer.
- Put the dimer to the field, matching coinciding parts.

Interestingly, evaluation with tracking cell trajectories shows that all elementary spaceships in the zig-zag expansion are constantly exchanging cells.
Slow chain spaceship
The slow chain can be built from the repetitions of the lightest spaceship F. Unlike the fast chains, chains with different slant can't be connected, so no zig-zags here. Same as its monomer, these spaceships have period 368 and velocity c/184.



Comments